Modellierungsprozess

Probleme bei vernachlässigter Datenmodellierung

Ohne korrekter Datenmodellierung entstehen in der Praxis oft die folgenden Probleme:

• Falsche logische Datenschemata werden in ein Datenbankmanagementsystem abgebildet, was zu redundanter Datenhaltung führt.
• Infolgedessen entstehen Inkonsistenzen durch Einfüge-, Update- oder Löschanomalien.
• Der Ursache liegt darin, dass die Relationen nicht in dritter Normalform sind. Die dritte Normalform fordert, dass ein Nichtschlüsselattribut nur direkt von einem Primärschlüssel (bzw. einem Schlüsselkandidaten) abhängig sein darf.
• Durch das Erstellen eines ER-Diagramms können solche Fehler schon frühzeitig vermieden werden.

Attribute, Attributwerte

Darstellung in Tabellenform:

• e1: (Meyer, 411, MA, 4000)
• e2: (Meyer, 412, MA, 4000)
• e3: (Müller, 409, MA, 5000)

Schlüssel

Gegeben  E: < A >

• Jedes Entity eines Typs ist eindeutig durch das zugeordnete Tupel beschrieben.
  (sonst wäre A nicht charakteristisch [genug] für E!)

aber

• Oft genügt ein Teil des Tupels zur Identifikation innerhalb dieses Objekt-Typs.

Schlüssel K (englisch: key) für E : <A>

Eigenschaften von Schlüsseln

K⊆A ist "Schlüssel" für E :  <A>         <=>

• (K1) K ist "identifizierende" Attributkombination für E : <A>,
         (d.h. verschiedene Objekte der realen Welt haben auch verschiedene Attributwerte bzgl. K)
• (K2) Es gibt keine echte Teilmenge  K' ⊂ K, für die Eigenschaft (K1) gilt (d.h. K ist minimal mit Eigenschaft (K1)).

Das bedeutet ein Schlüssel muss ein Objekt (Entity) eindeutig identifizieren können und zweitens minimal sein. D.h. es ist nicht möglich einen Teil des Schlüssels wegzulassen ohne das die erste Eingenschaft verloren geht.

Beispiel:

Angestellte : < Name, AngNr, Ort, Gehalt, GebDatum >
{AngNr} ist Schlüssel
{Name, GebDatum} evtl. Schlüssel

Primärschlüssel

Es kann mehrere Schlüssel, d.h. Attribute (Attributkombinationen) mit den vorher genannten Eigenschaften (K1) und (K2) geben. Diese nennt man auch Schlüsselkandidaten.

Einen davon definiert man als Primärschlüssel (Primary Key) fest.

Besonders bequem ist die Verwendung eines einfachen Schlüsselattributes wie zum Beispiel AngNr, AbteilungsNr, ArtikelNr, etc. anstelle einer mehrstelligen Attributkombination.

Hinweis: Im ER-Modell bzw. auch bei Schemadefinitionen werden Attribute, die den Primärschlüssel bilden, oft unterstrichen dargestellt.

Beziehungen

Beziehung (relationship) (b):

Zwei oder mehr Objekte können miteinander in Beziehung stehen

Beispiele:

• Angestellter 411 gehört zu Abteilung 2
  b1 = (Angestellter 411, Abteilung 2)
• Teil x wird benötigt zur Herstellung von Teil y
  b2 = (x, y)
• Lieferant Meyer liefert Bauteil "Gehäuse" für Produkt "Getriebe"
  b3 = (Lieferant Meyer, Bauteil "Gehäuse", Produkt "Getriebe")

Anzahl n der an einer Beziehung beteiligten Entities (bzw. Entitätstypen) ist der Grad dieser Beziehung.

(n = 2: binäre Beziehung).

Menge von Beziehungen

Menge von Beziehungen: (B^t)

Beziehungen desselben Grades und derselben Bedeutung zum Zeitpunkt t können (analog zu Entities) zu Mengen B^t zusammengefasst werden.

Beispiele:

• Menge aller Zugehörigkeiten (Angestellter, Abteilung)
  {(Angestellter 47, Abteilung 11), (Angestellter 08, Abteilung15), ...}
• Menge aller LV-Besuche (Student, Lehrveranstaltung)
  {(9851765, LV-1742), (0705375, LV-1802), (0812484, LV-1802), ...}
• Menge aller Lieferungen (Lieferant, Bauteil, Projekt)

Beziehungstypen

Beziehungstyp (relationship-type) (B):

Charakterisierung der Beziehungsmengen durch geeignete Eigenschaften.

B = Name des Beziehungstyps

Beispiele:

• Zugehörigkeit: Angestellter gehört zu Abteilung.
• Besucht: Student besucht Lehrveranstaltung.
• Mitarbeit: Angestellter arbeitet an Projekt mit.

Attribute von Beziehungstypen

Beziehungstypen können ebenso wie Entitäts-Typen Attribute haben.

Es sollen sprechende Bezeichnungen für die Attribute gewählt werden.

Beispiele:

• seit_wann: Dauer der Abteilungszugehörigkeit oder besser noch: Seit wann ist jemand bei der Abteilung
• umfang: Umfang der Mitarbeit an einem Projekt
• fehlstunden: Anzahl der Fehlstunden (bei Beziehung Student besucht LV)
• menge: Menge des durch einen Kunden bestellten Artikels

Diese Attribute werden einer konkreten Beziehung zugeordnet, d.h. sie dienen nicht zur unterscheidenden Charakterisierung der Beziehung!

Grafische Darstellung nach Chen

Grafische Darstellung - Hinweise

Die Angabe aller Attribute ist bei größeren Diagrammen unübersichtlich.

Empfehlung:

• Anfertigen von Auszügen mit Angabe der Attribute
• Im Gesamt-Diagramm eventuell lediglich Schlüsselattribute und Attribute von Beziehungstypen angeben
• Beziehungstypen durchnumerieren und gesondert auflisten mit Angabe ihrer Bedeutung bzw. des Namens

ER-Diagramm

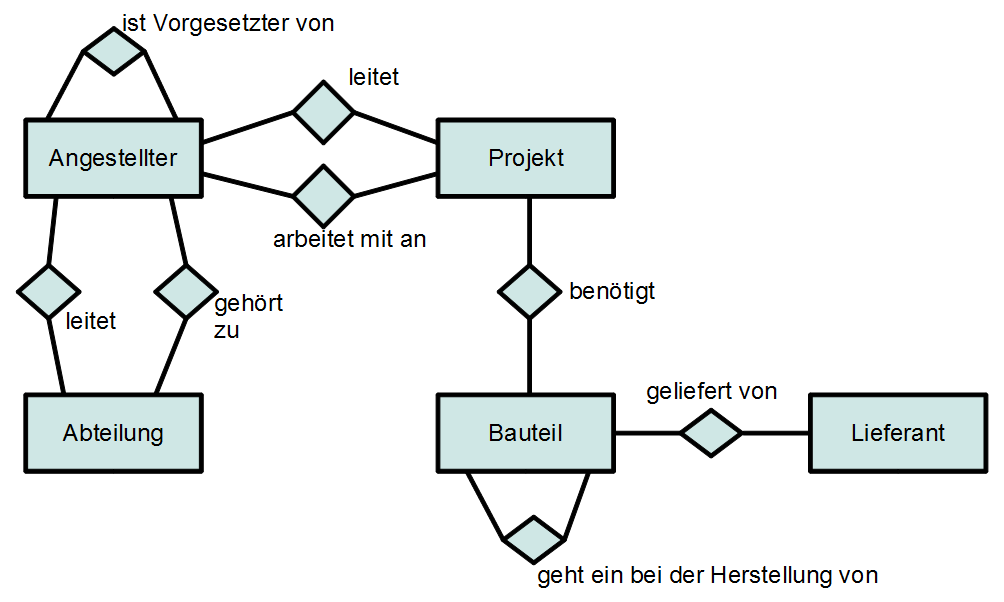
Höhergradige Beziehungen

Eine Beziehung dritten Grades hat man wenn man z.B. modellieren will, dass ein Lieferant für Projekte bestimmte Teile liefert:

Spezialisierung und Generalisierung

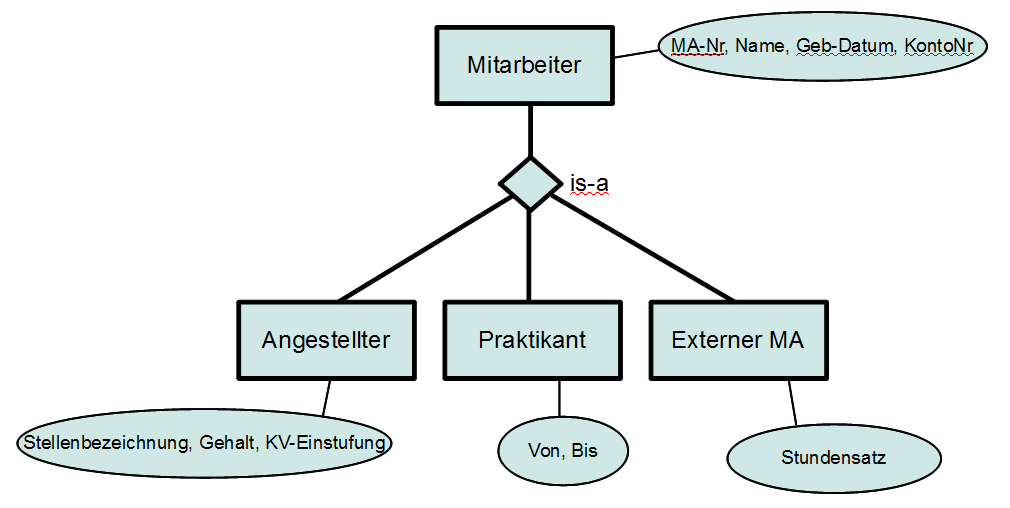
Mittels der is-a-Beziehung lässt sich die Spezialisierung und Generalisierung abbilden. Die untergeordneten Entitätstypen erben dabei die Attribute und den Primärschlüssel des übergeordneten Entitätstyps.
Es existieren viele unterschiedliche Notationsformen um diesen Spezialfall abzubilden (z.B. Pfeile vom Untertyp zum Obertyp statt der is-a Beziehung)

Kardinalität von Beziehungen

Üblicherweise gelten für Beziehungstypen bestimmte Bedingungen, die die möglichen Kombinationen zwischen Objekten in einer Beziehung beschränken:

Die Komplexität einer Beziehung wird durch Angabe von Kardinalitäten bestimmt.

Im folgenden wird die 1:n-Notation verwendet, die die folgenden Variationen für Beziehungen 2. Grades vorsieht:

• 1:1
• 1:n bzw. n:1
• m:n

Diese Notation macht keine Aussage darüber ob ein Objekt an einer Beziehung beteiligt sein muss (zwingende/optionale Beziehungen). Dafür existieren andere Notationen wie z.B. die (min,max)-Notation, UML oder die Krähenfußnotation.

Kardinalität von Beziehungen

Beziehungen vom Grad 2

• 1:1 Ein Objekt des Typs E1 steht mit höchstens einem Objekt des Typs E2 in Beziehung (und umgekehrt).
• 1:n Ein Objekt des Typs E1 kann mit einer beliebigen Anzahl von Objekten des Typs E2 in Beziehung stehen. Ein Objekt des Typs E2 kann mit höchstens einem Objekt des Typs E1 in Beziehung stehen.
  "n" steht für eine beliebige ganze Zahl ≥0 ("beliebig viele")
• n:1 Umkehrung von 1:n
• m:n Ein Entity des Typs E1 kann mit mehreren anderen Entities des Typs E2 in Beziehung stehen (und umgekehrt).
  "m" und "n" steht für beliebig viele

ER-Diagramm mit Kardinalitäten

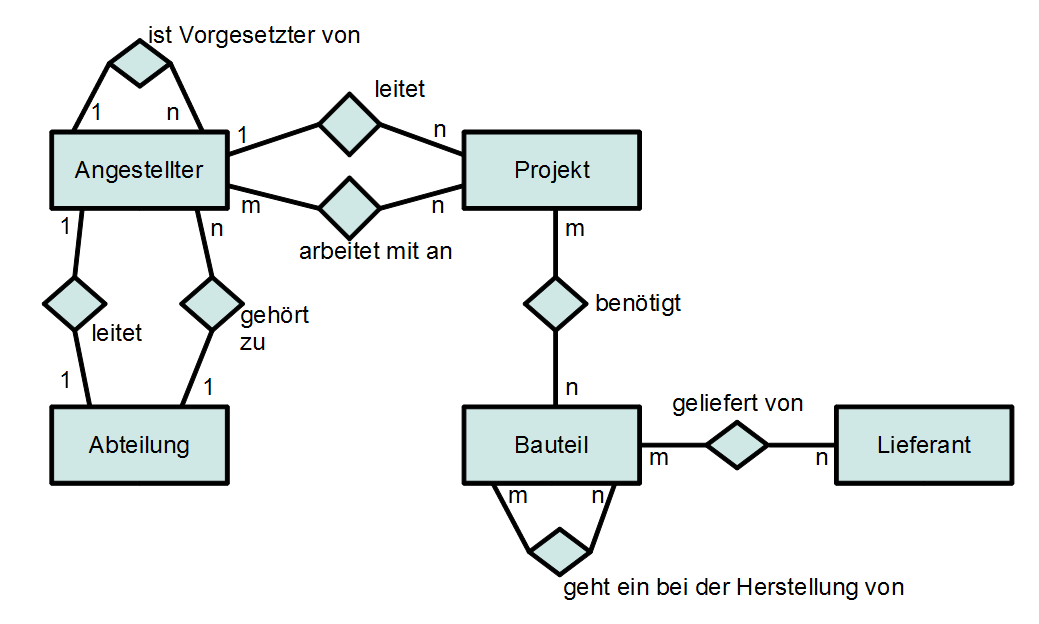
Erweiterung: (min, max) - Kardinalitäten

Weitere Angaben der Kardinalität eines Entity-Typs E in einem Beziehungstyp B als Zahlenpaar (α, β) mit 0 ≤ α ≤ β

Ein Objekt e (vom Typ E) gehört zu mindestens α, maximal β Beziehungen des Typs B.

⇒ Angabe, ob alle Entities eines Typs Beziehungen dieses Typs haben müssen.

Erweiterung: (min, max) - Kardinalitäten

Schreibweisen:

"*"    = beliebig viele

(1, 1): ein Entity hat zu einem bestimmten Zeitpunkt genau eine Beziehung.

(0, *): ein Entity kann zu jedem Zeitpunkt beliebig viele Beziehungen haben; muss aber nicht in einer Beziehung stehen.

üblich: (0,1), (0,*), (1,1), (1,*)

(d.h. im allgemeinen beschränkt man sich auf diese Spezialfälle)

Erweiterung: (min, max) - Kardinalitäten

Die folgende Abbildung zeigt wie die (min, max)-Notation bei einer Beziehung zweiten Grades mit der 1:n-Notation zusammenhängt:

ER-Modell mit (min, max) Kardinalitäten

Krähenfußnotation - Beispiel

Eine Person ist geboren in minimal einem, maximal einem Ort. Eine Person ist gestorben in minimal Null, maximal einem Ort. Eine Person macht Ferien in minimal Null, maximal vielen Orten. Eine Person war bereits in minimal einem, maximal vielen Orten. Annahme: In die Gegenrichtung kann pro Ort nur exakt eine Person zugeordnet werden (Annahme nicht wirklich plausibel).